Amazing tree —— 二叉查找树

二分查找很好的解决了查找问题，将时间复杂度从 O (n) 降到了 O (logn)。

但是二分查找的前提条件是数据必须是有序的，并且具有线性的下标。对于线性表，可以很好的应用二分查找，但是在插入和删除操作时则可能会造成整个线性表的动荡，时间复杂度达到了 O (n)，链表更是没法应用二分查找。

于是有了下面将要介绍的算法，其在查找、插入、删除都能够达到 O (logn) 的时间复杂度 —— 二叉查找树

见名知意，其数据结构基础为二叉树，初次接触到二叉树时并没有感觉到其有什么突出之处。但看到通过二叉树构建出的二叉查找树方案时，确被深深的震撼了。

定义

二叉查找树（英语：Binary Search Tree），也称二叉搜索树、有序二叉树（英语：ordered binary tree），排序二叉树（英语：sorted binary tree），是指一棵空树或者具有下列性质的二叉树：

若任意结点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；

若任意结点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

任意结点的左、右子树也分别为二叉查找树；

没有键值相等的结点。

根据上面的规则我们先来定义一颗二叉树

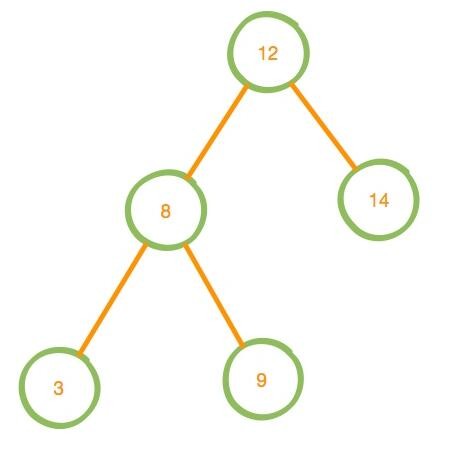
插入

现在再插入一个元素 13。 13>12 所以往右边走来到 14，13 < 14 则左走，发现 14 没有左孩子，所以将 13 插入之，得到下面这张图

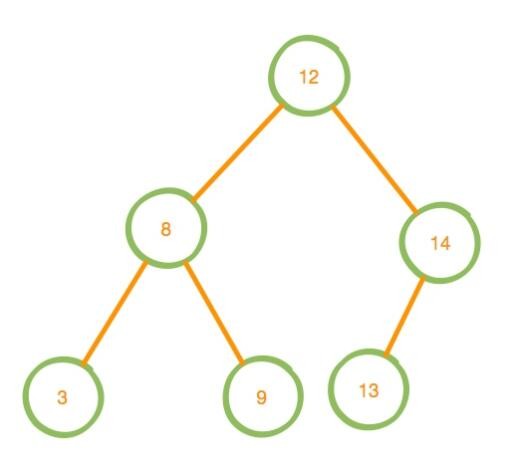
查找

按照上面插入的思路，可以很容易实现搜索操作。并且发现其查找的时间复杂度就为这颗树的深度。

根据完全二叉树的性质，具有 n 个结点的完全二叉树的深度为 [logn] + 1

忽略掉 +1 得到二叉查找树的查找时间复杂度为 O(logn)，但是实际上并非如此，后面我们分析。

遍历

二叉树的遍历有前序、中序、后序遍历三种方式，这里着重介绍后序遍历。

对二差查找树进行中序遍历时，可以得到一个 asc 的排序结果。如上面的树中序遍历的结果是 3, 8, 9, 12, 13, 14。

中序遍历从一颗子树最左的节点开始输出，既该树的最小值。实现中序遍历只需要将数据收集点置于左递归点与右递归点之间，这样说还是有些含糊了，看代码吧

/**
 * 中序遍历
 * @param $root
 * @return array
 */
public function inorder($root)
{
    $data = [];

    if ($root->left) {
        $data = array_merge($data, $this->inorder($root->left)); //左孩子递归点
    }

    $data[] = $root->data; // 这里是中序遍历的数据收集点

    if ($root->right) {
        $data = array_merge($data, $this->inorder($root->right)); // 右孩子递归点
    }

    return $data;
}

前驱与后继， 以 9 节点为例， 12 属于 9 的后继，8 属于 9 的前驱。

删除

我们给这颗树多加几个结点

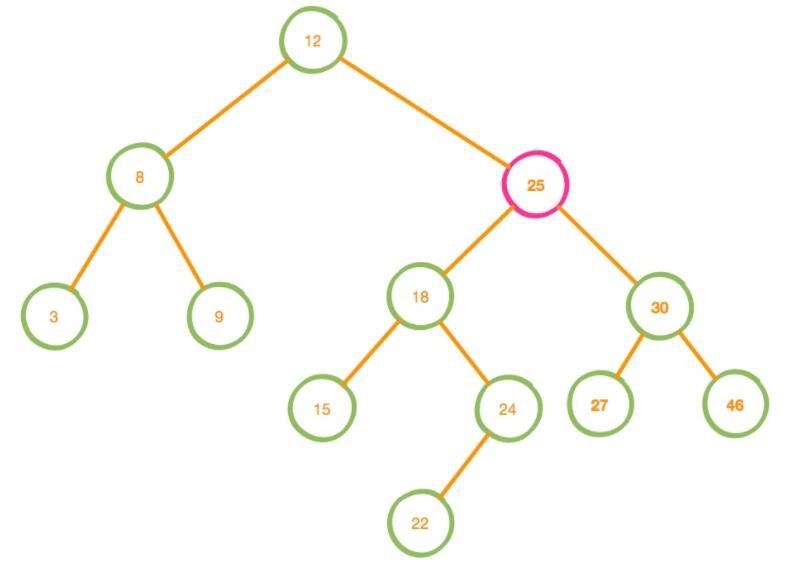
删除树中的结点分为很多种情况，如被删除的结点不存在子结点，只存在左子树 / 右子树，左右子树都存在，这里已覆盖率最广的左右子树都存在为例。

分析一个需求时要并不是需求存在多少中情况我们就写多少种情况。而应该分析情况之间的关系，是否存在重复，或者属于关系等，程序员应该做的就是提取需求的本质，力求于最简洁的实现

现在我们打算删除 25 这个结点，你会怎么做？

如果只是简单把 18 来顶替原来 25 的位置，则需要对 18 这颗子树的孩子们进行重新调整。18 只有三个孩子还好，但是当孩子成千上万时，显然会造成大面积的调整。

所以我希望能够找到一个更好的节点来代替 25，按照算法导论中的描述，我们应该寻找该结点的前驱或者后继来代替，比如图中的 24 和 27 分别是 25 的前驱和后继。

为什么要使用前驱或者后缀来代替？这点我十分不确定，我给自己的理由是

该结点是一个特殊值，属于某颗子树的最大值或者最小值，具有确定性，可以被比较好的定义且查找出来。

由于该结点属于被删除节点的前驱或者后继，则删除该结点对数据结构造成的影响最小。我并不确定是对什么的数据结构造成的影响最小

上面描述的情况的图解如下

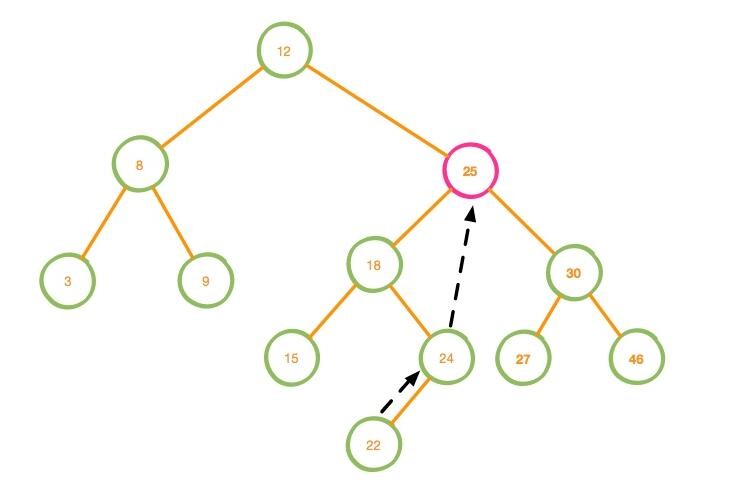
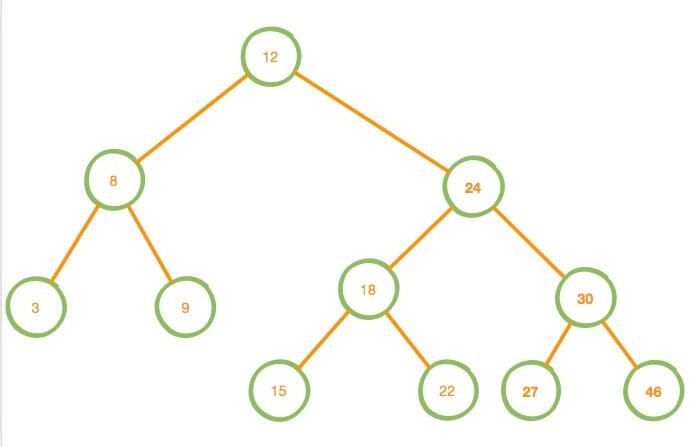
删除还存在一些其他的情况，比如下面这种情况↓

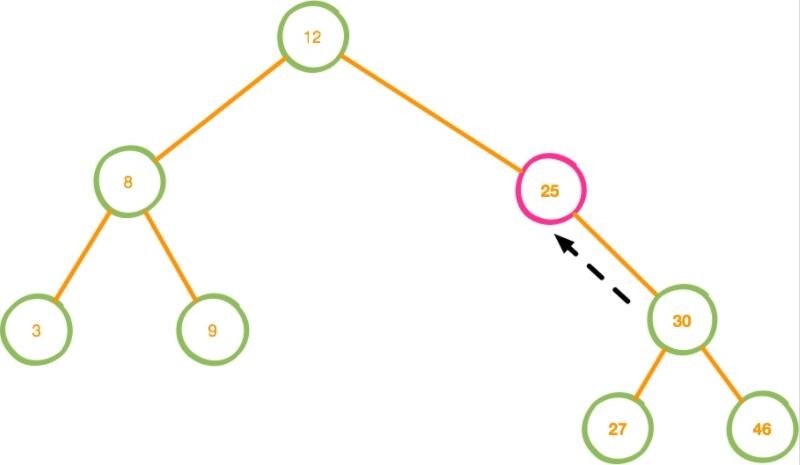
对于这种情况直接将 30 提升到 25 即可，接下来看一下看 php 的代码实现：

public function delete($root, $data)
{
        if (!$root) {
                return null;
        }

        if ($root->data === $data) {
                if ($root->left) {
                        // 左转
                        $node = $root->left;

                        $parent = $root;
                        $toward = 'left';

                        while ($node->right) {

                                $parent = $node;
                                $toward = 'right';

                                $node = $node->right;
                        }

                        $root->data = $node->data;

                        $parent->{$toward} = $this->delete($node, $node->data);

                } else {
                        return $root->right;
                }
        } elseif ($root->data > $data) {
                // 如果root的左孩子没有被删除,那就原样返回回来, 如果被删除了,那就找个孩子代替
                $root->left = $this->delete($root->left, $data);
        } else {
                $root->right = $this->delete($root->right, $data);
        }

        return $root;
}

由于 php 有内存回收机制，因此我们没有办法像 c 一样直接去修改内存，所以这里借助递归的特性来解决这个问题 $root->left = $this->delete($root->left, $data); 做类似这样一个处理，这可能会有些理解上的困难。但总归还是能够明白的～

除了递归解决外，也可以用下面这种办法。

即定义一个 parent 和 toward 来做一个导向，这在上面的代码中也有体现。该方法更加适用于迭代处理

$parent = $root;
$toward = 'left';

while ($node->right) {

    $parent = $node;
    $toward = 'right';

    $node = $node->right;
}

补充

由于 php 没有像 js 一样的字面量对象或者 c 一样的 struct。因此直接使用对象来表示树中的结点

class BiTNode
{
    public $data;
    public $left;
    public $right;

    public function __construct($data, $left = null, $right = null)
    {
        $this->data = $data;
        $this->left = $left;
        $this->right = $right;
    }
}

在查找的时候指出了，二叉查找树的查询的时间复杂度并不是严格意义上的 O (logn) 是因为有这样的情况发生， 假设需要插入 12, 10, 9, 5, 4, 1 这几个数据，那么我们会得到这样一颗歪脖子树

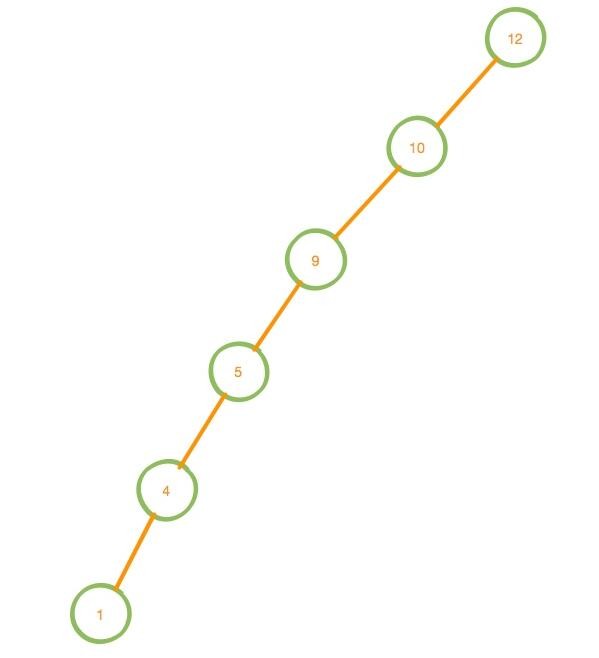
此时的时间复杂度俨然已经变成了 O (n)，不过对于这样的问题自然已经有解决方案。下一节将会在 AVL 树和红黑树这两种解决方案中选一种来 BB~

当然二叉查找树依旧是各种树的根基，还请认真理解。

附图：

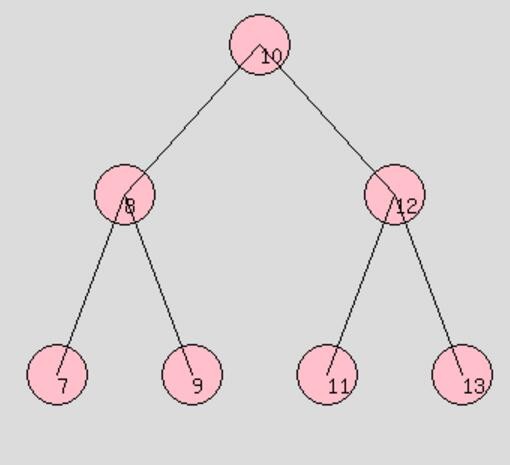
深度优先遍历：

前序遍历：10 8 7 9 12 11 13

中序遍历：7 8 9 10 11 12 13

后序遍历：7 9 8 11 13 12 10

广度优先遍历：

层次遍历：10 8 12 7 9 11 13

二叉树的深度优先遍历的非递归的通用做法是采用栈，广度优先遍历的非递归的通用做法是采用队列。

class Node{
    public $value;
    public $left;
    public $right;
}
//先序遍历 根节点 ---> 左子树 ---> 右子树
function preorder($root){
    $stack=array();
    array_push($stack,$root);
    while(!empty($stack)){
        $center_node=array_pop($stack);
        echo $center_node->value.' ';//先输出根节点
        if($center_node->right!=null){
            array_push($stack,$center_node->right);//压入左子树
        }
        if($center_node->left!=null){
            array_push($stack,$center_node->left);
        }
    }
}
//中序遍历，左子树---> 根节点 ---> 右子树
function inorder($root){
    $stack = array();
    $center_node = $root;
    while (!empty($stack) || $center_node != null) {
             while ($center_node != null) {
                 array_push($stack, $center_node);
                 $center_node = $center_node->left;
             }

             $center_node = array_pop($stack);
             echo $center_node->value . " ";

             $center_node = $center_node->right;
         }
}
//后序遍历，左子树 ---> 右子树 ---> 根节点
function tailorder($root){
    $stack=array();
    $outstack=array();
    array_push($stack,$root);
    while(!empty($stack)){
        $center_node=array_pop($stack);
        array_push($outstack,$center_node);//最先压入根节点，最后输出
        if($center_node->left!=null){
            array_push($stack,$center_node->left);
        }
        if($center_node->right!=null){
            array_push($stack,$center_node->right);
        }
    }

    while(!empty($outstack)){
        $center_node=array_pop($outstack);
        echo $center_node->value.' ';
    }

}
$a=new Node();
$b=new Node();
$c=new Node();
$d=new Node();
$e=new Node();
$f=new Node();
$a->value='A';
$b->value='B';
$c->value='C';
$d->value='D';
$e->value='E';
$f->value='F';
$a->left=$b;
$a->right=$c;
$b->left=$d;
$c->left=$e;
$c->right=$f;
preorder($a);//A B D C E F
echo '<hr/>';
inorder($a);//D B A E C F
echo '<hr/>';
tailorder($a);//D B E F C A